Noter og hjælp til skole også ellers sjove ting der sker på mit uddannelses forløb. Det er gratis hjælp og eksempler på opgaver :)
Søg i denne blog
tirsdag den 20. maj 2014
Formler i Vø
Eller
Overskudgrad*aktivernes omsætning-hastighed
Overskudsgrad= Resultat af primærdrift*100/nettoomsætning
Hvis finansielle indtægter er der
(Resultat af primærdrift+finansielle indtægter)*100/nettoomsætning
Aktivernes Omsætnings-hastighed= Nettoomsætning/Gennemsnitlige Aktiver
Egenkapitalens Forrentning = Resultat før skat *100/Gennemsnitlige egenkapital
eller
Afkastningsgrad + (afkastningsgrad - gældsrente) * gearing
Gearing = Gennemsnitlige gælds-forpligtelser/Gennemsnitlig egenkapital
Gældrente= Finansielle omsætninger * 100/gennemsnitlige gældsforpligtelser
fredag den 28. marts 2014
Forskellige Lån og Amortisationstabel
Det er en plan over et låns afvikling
Annuitetslån Er lån hvor ydelsen er den samme hver termin
Serielån
Er et lån hvor afdragene er de samme hver termin
Stående lån
Det er et lån hvor man ikke betaler afdrag, man betaler kun renter. Og så afdrager man hele lånet den sidste termin.
Link
Amortisationstabel Beregner
laankontanter.dk/amortisationsudregner
fredag den 21. marts 2014
Annuitets regning
En annuitet er en række af betalinger
Fremtidsværdi af annuitet formel
y= terminsydelse (det man indsætter hver termin)
n =Antal terminer
r= rente i kommatal
An=fremtidsværdi af annuiteten
A0= nutidsværdi af annuiteten
torsdag den 20. marts 2014
Effektiv rente:
Den effektive rente i pr. n terminer beregnes som
Formel til effektiv rente
i=(1+r)n-1
Eksempel
Renten er 1% pr måned i 12 måneder
i=(1+0,01)12-1=12,68%
Formel til gennemsnitlig rente
Gennemsnitlig rente
Hvis der tilskrives renten ri i periode i kan gns. Rente beregnes som
Formel til og beregne gennemsnit af procent.
Eksempel
Procenter 2%, 5%, 9%
Gennemsnit rente eksempel
fredag den 14. marts 2014
Finansiel regning
Kapitalformel
Kn=K0*(1+r)n
Kn=slutkapital (Det der står på kontoen efter en termin)
K0 = Startkapital (Begyndelseskapital det jeg sætter ind til at starte med)
n = antal terminer (Antal gange man får tilskrevet renter)
r= renteprocenten i kommatal
fredag den 31. januar 2014
Diskrete og Kontinuente observationer
Diskrete Observationer
Variationsbredden =største- mindste observation
Kvartilafstand = 3kvartil - 1 kvartil
Kontinuente Observationer
Variationsbredden =Største interval midtpunkt - mindste interval midtpunkt
Kvartilafstand = 3kvartil - 1 kvartil
torsdag den 30. januar 2014
Kontinuente observationer
Grupperede observationer
Nab grupperer observationer i nogle intervaller
Interval frekvens
Summeret interval frekvens
Middeltal = gennemsnit
Hvor mi er intervalmidtpunkt
A - fraktilen er den mindste værdi xi hvor fi=a
Typeinterval
Er det interval der forekommer oftest
Diagram med frekvens op af y-aksen kaldes et søjlediagram
Diagram med summeret frekvens op ad y aksen kaldes en sumkurve
torsdag den 23. januar 2014
Statistik
Diskrete observationer (x;)
Har et endeligt antal niveauer (f.x. antal søskende, slå med en terning o lig.)
Kontinuerte observationer (x;)
Kan måles på en talskala med kommatal (f.x. Højde, Vægt)
Frekvens (f;)
Den relative hyppighed =hyppighed divideret med hyppighed i alt. Dvs fi=
Summeret frekvens (fi):
Summen af frekvenserne op til den i´te observationer
Fi=∑fi
Pindediagram = histogram:
Frekvens op af y-aksen, og xi på x-aksen
Trappediagram
Summeret frekvens op af y- aksen. Og x; på x aksen.
Gennemsnit =middelværdi=middeltal
Beregnes ved at lægge alle observationer sammen og dividere med antallet. Kan også beregnes som ∑xi*fi eller
A- fraktilen
(0<a<1) er den mindste observation hvor fi>a
Kvartilsæt =
1 kvartil = 25% fraktil
2 kvartil = 50% fraktil = median
3 kvartil = 75% fraktil
Median
Midterste observation
Typetal
Den observation der forekommer oftest.
lørdag den 18. januar 2014
Learnamark Terminal server Vejledning
Gå på skolen netværk/computer hjemme fra eller fra din egen computer
torsdag den 9. januar 2014
Potensfunktioner v2.1
Potensfunktioner
En potensfunktion er en funktion med den generelle forskrift:
F(x)=b*xa hvor x>0 og b>0
Hvis a>0 er funktionen voksende
Hvis a<0 er funktionen aftagende
F(1)=b Dvs. b=y værdien når x=1
Finde forskrift ud fra 2 punkter
Hvis vi kender 2 punkter på funktionen
(x1,y1) og (x2,y2) så kan a og b findes som
Løsning af potens ligninger
Hvis man har en ligning på formel
Xn=a så kan den løses
N og a er tal
Eksempel
2*x7=10
X7=5
Procentvise ændringer
Hvis x ændres med rx% og der gælder
ry=(1+rx)a-1
rx og ry er procenten i kommatal
Eksempel
Forskriften f(x)=3*x0,75
| x | 1 | 1,2 | 1,44 | 1,728 |
| F(x)=3*x0,75 | 3 | 3,3496 | 3,9436 | 4,5215 |
| Forskel | ______ | 0,4396 | 0,5040 | 0,5779 |
| Forskel i % | ______ | 14,65% | 14,65% | 14,65 |
Potensfunktioner
Potensfunktioner
En potensfunktion er en funktion med den generelle forskrift:
F(x)=b*xa hvor x>0 og b>0
Hvis a>0 er funktionen voksende
Hvis a<0 er funktionen aftagende
F(1)=b Dvs. b=y værdien når x=1
Finde forskrift ud fra 2 punkter
Hvis vi kender 2 punkter på funktionen
(x1,y1) og (x2,y2) så kan a og b findes som
b=y1*x1-a
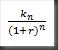

![clip_image002[1] clip_image002[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjrYdxHF9zv0veaCva-ltwkT0dQA07vmB1crBDTWHBKXIp5h3N-cpwOYi9n-CGl5_GwIO_3oYzLqCnYv5h4kRTiXD8CDLsGEAGlg3zqmtlK1ucylkrIrkXHSUWBjqzq5posgm1eb9mo9UxH/?imgmax=800)

